Unidad 3 Modelos Aditivos Generalizados
María Victoria Quiroga4
Instituto Tecnológico de Chascomús (INTECH, UNSAM-CONICET), Escuela de Bio y Nanotecnologías (UNSAM)
3.0.1 Aclaración
En esta unidad se utiliza el paquete ggplot2 (Wickham 2016) para generar algunos gráficos. Para comprender el código empleado se recomienda leer el Capítulo 3: Data visualization del libro R for Data Science (Wickham and Grolemund 2017).
3.1 ¿Por qué usar Modelos Aditivos Generalizados (GAMs)?
- La relación entre variables predictoras (i.e., independientes) y la variable respuesta (i.e., dependiente) no necesita ser lineal.
- No necesitamos conocer de antemano la forma funcional de la relación.
- Son modelos muy flexibles que permiten la interpretación (de manera gráfica) de los efectos parciales de cada variable independiente.
- Podemos:
- Incluir predictores categóricos e interacciones.
- Usar distribuciones diferentes a la normal para la variable dependiente.
- Incluir correlaciones entre observaciones (e.g., medidas repetidas, diseños anidados) -modelos mixtos.
3.2 ¿Qué son los GAMs?
Los GAM permiten incorporar los efectos additivos de distintas variables independientes (i.e., explicativas) utilizando funciones suaves (\(smooth functions\)).
\[ g(\mu) = \beta_0 + f_{1}(x_{1}) + f_{2}(x_{2}) + ... + f_{n}(x_{n}) + \varepsilon \]
Donde \(\mu\) es el valor esperado de la variable dependiente y que puede presentar distribuciones de la familia exponencial, g es la función de enlace, \(\beta_0\) es el intercepto, \(x_{n}\) son las n variables independientes y cada \(f_{n}\) es una función suave que se estima de manera no paramétrica. Se pueden incluir funciones suaves para interacciones, por ejemplo entre las variables independientes 1 y 2 \(f(x_{1},x_{2})\). Si se incluyen términos aditivos aleatorios, por ejemplo la autocorrelación en series de tiempo, se generan modelos mixtos (GAMM, generalized additive mixed model).
Existen diferentes estrategias para ajustar una curva suave y continua a los datos. Aquí vamos a utilizar splines, y en particular spline cúbico y cúbico cíclico. De manera muy breve, un spline cúbico es una curva suave cúbica por tramos (Figura 3.1). El spline cúbico cíclico empieza y termina en el mismo punto. El paquete con el que vamos a trabajar mgcv (Wood 2017) usa splines penalizados ( conventional intergrated square second derivative cubic spline penalty), donde la penalización será más grande cuanto menos suave sea la curva.
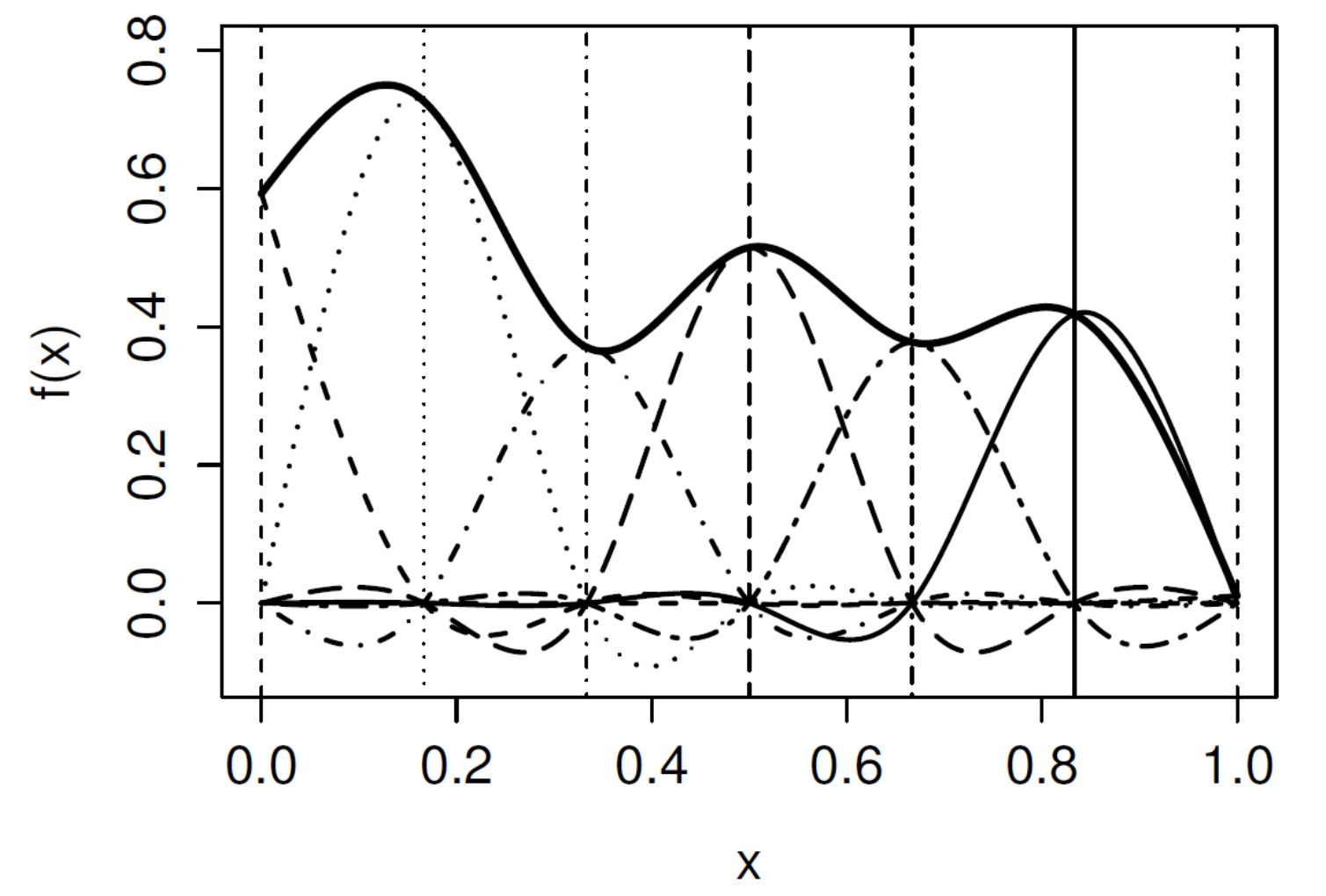
Figure 3.1: Construcción de un spline cúbico. La curva suave (línea contínua gruesa) es la suma de las 5 funciones basis (líneas finas). Las líneas verticales muestran los nodos equiespaciados. Extraído de Wood (2017).
3.3 ¡Manos a la obra!
Utilizaremos un set de datos del trabajo The dynamics of picocyanobacteria from a hypereutrophic shallow lake is affected by light-climate and small-bodied zooplankton: a 10-year cytometric time-series analysis publicado en FEMS Microbiology Ecology (Quiroga et al. 2021), disponibles en el Repositorio Institucional CONICET Digital.
Descargar el set de datos data_gam.csv de GitHub Limno-con-R/CILCAL2023. Guardar el archivo en una carpeta llamada data, dentro del Directorio de Trabajo del Proyecto que creamos para esta Unidad (ver cómo hacerlo en la Unidad 1).
Instalar los paquetes como se indica en la Unidad 1. Luego, cargarlos en la sesión
library(mgcv)
library(ggplot2)
library(itsadug)
library(data.table)
library(car)
library(grid)
library(lubridate)Leer datos, dar formato as.Date a la fecha y generar las variables Mes y Dias.
base <- read.csv("data/data_gam.csv")
base$Fecha <- as.Date(base$Fecha, "%m/%d/%Y") # formato de fecha en inglés
base$Mes <- as.numeric(format(base$Fecha,'%m')) # generar variable Mes
base$Dia1 = rep(base$Fecha[1], nrow(base)) # fecha inicial de la serie
base$Dias <- (interval(base$Dia1, base$Fecha) %/% days(1))+1 # generar variable DiasInspección visual de primeras filas de la tabla. Para ver toda la tabla se puede utilizar View(base).
head(base)## Fecha Pcy_orgml Mes Dia1 Dias
## 1 2007-05-22 6660000 5 2007-05-22 1
## 2 2007-06-05 6830000 6 2007-05-22 15
## 3 2007-06-21 4700000 6 2007-05-22 31
## 4 2007-07-03 4680000 7 2007-05-22 43
## 5 2007-07-17 6500000 7 2007-05-22 57
## 6 2007-07-31 8110000 7 2007-05-22 71Ver la estructura de los datos
str(base)## 'data.frame': 225 obs. of 5 variables:
## $ Fecha : Date, format: "2007-05-22" "2007-06-05" ...
## $ Pcy_orgml: num 6660000 6830000 4700000 4680000 6500000 8110000 8840000 11000000 10100000 6340000 ...
## $ Mes : num 5 6 6 7 7 7 8 8 9 9 ...
## $ Dia1 : Date, format: "2007-05-22" "2007-05-22" ...
## $ Dias : num 1 15 31 43 57 71 85 99 113 127 ...base es un objeto data.frame con 225 obs. observaciones o filas y 5 variables o columnas.
Variables: Fecha con formato Date. Pcy_orgml, abundancia de picocianobacterias (organismos/ml) en la laguna Chascomús, como valores numéricos num.
Se generaron las variables Mes y Dias como números num. Mes indica el #mes (1-12) de la fecha de muestreo y Dias indica el #días transcurridos desde la primer fecha (considerando la primer fecha como día #1).
Grafico exploratorio de la serie temporal
ggplot(base, aes(x= Dias, y= Pcy_orgml)) +
geom_point() +
geom_line()+
theme(legend.position = "none")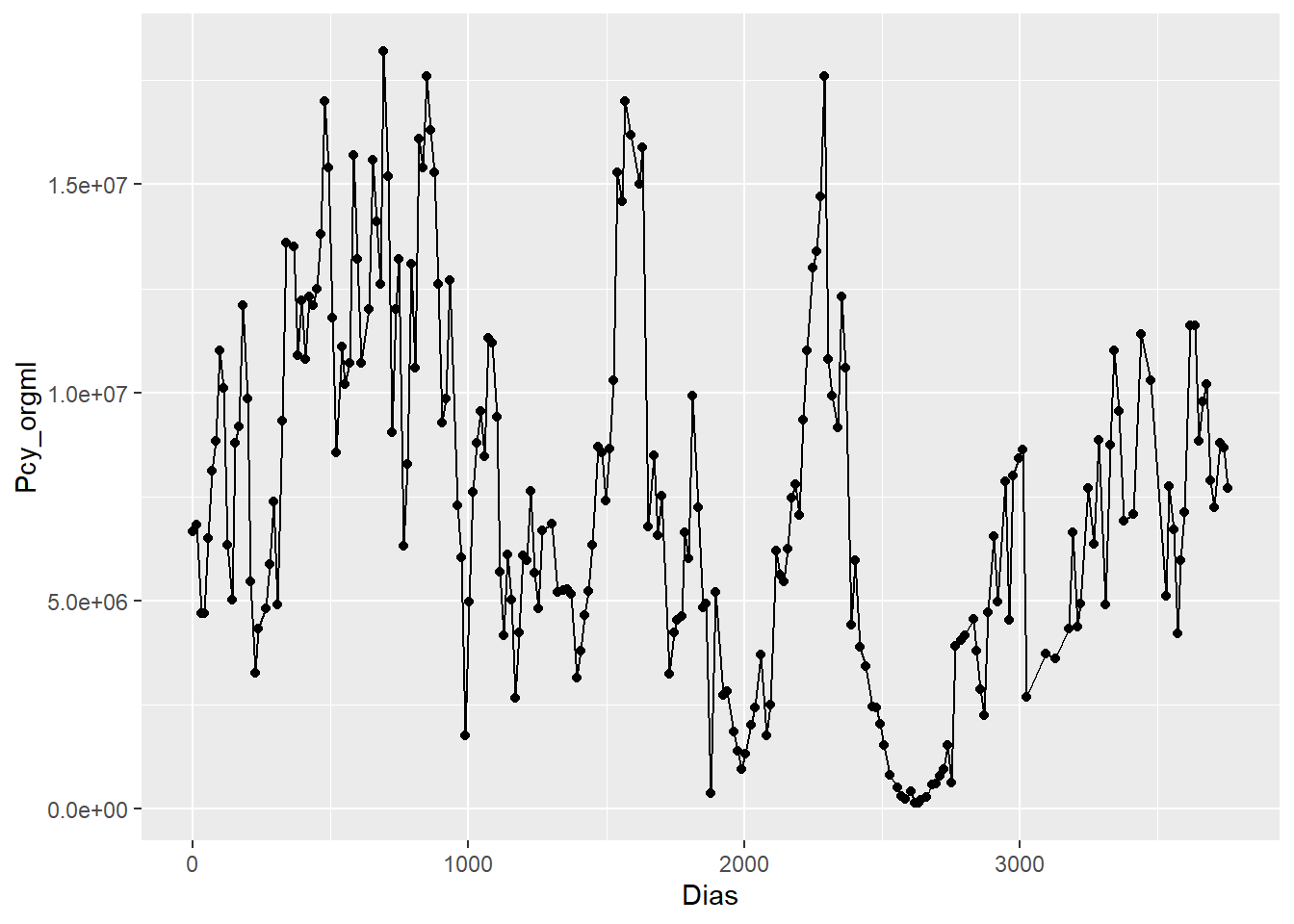
Figure 3.2: Serie temporal de abundancia (organismos/ml) de picocianobacterias.
No se observan outliers en el gráfico.
Para datos de conteo (e.g., organismos/ml) generalmente se utiliza la distribución de Poisson, pero las series temporales de abundancia de microorganismos suelen presentar sobredispersión (Figura 3.2). Para considerar una varianza mayor que la media se podría utilizar la distribución binomial negativa o la quasi-familia quasipoisson. En este ejemplo se implementará family=quasipoisson.
La autocorrelación temporal de los datos se incluye utilizando una estructura autorregresiva de primer orden continua correlation = corCAR1(form = ~ Dias) en un modelo mixto gamm().
Como primer modelado se generan funciones suaves s() para el efecto estacional Mes y el efecto interanual ( trend) Dias. Se utiliza spline cúbico cíclico para el primer efecto s(Mes, bs="cc") y cúbico para el segundo efecto s(Dias, bs="cr").
modelo1<-gamm(Pcy_orgml ~ s(Mes, bs = "cc") + s(Dias, bs="cr"),
family=quasipoisson, data = base,
correlation = corCAR1(form = ~ Dias))##
## Maximum number of PQL iterations: 20## iteration 1## iteration 2## iteration 3## iteration 4Por default el máximo número de iteraciones está seteado en 20 niterPQL=20. Si el modelo no converge se puede incrementar el número de interacciones, por ejemplo: gamm(..., niterPQL=40).
Interpretación visual de los efectos parciales: curvas suaves s() ( smooth functions)
plot(modelo1$gam, scale=0, scheme=1, pages=1)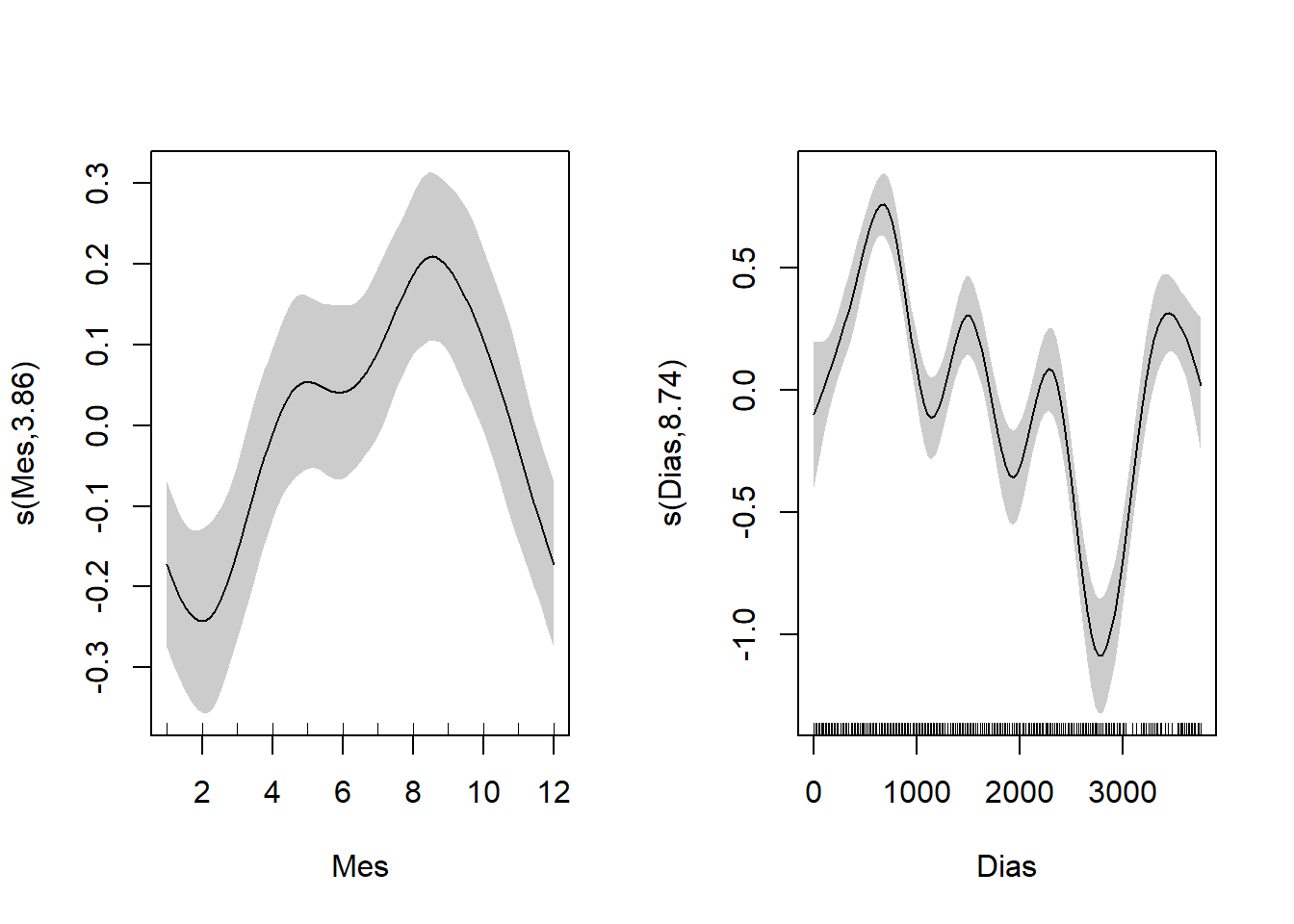
Figure 3.3: Efectos parciales del modelo 1. Las curvas suaves se centraron en cero, se indican los intervalos de confianza de 95% en gris. Las líneas internas en los ejes x (Mes y Dias) representan los datos.
Información del modelo
summary(modelo1$gam)##
## Family: quasipoisson
## Link function: log
##
## Formula:
## Pcy_orgml ~ s(Mes, bs = "cc") + s(Dias, bs = "cr")
##
## Parametric coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 15.72716 0.02977 528.2 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Approximate significance of smooth terms:
## edf Ref.df F p-value
## s(Mes) 3.858 8.000 3.674 3.46e-06 ***
## s(Dias) 8.743 8.743 23.752 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## R-sq.(adj) = 0.564
## Scale est. = 1.209e+06 n = 225Se especifica la familia que se utilizó ## Family: quasipoisson y la función de enlace ## Link function: log. ?family muestra las familias y funciones de enlace que se utilizan por default. Para cambiar la función de enlace solo hay que especificarlo en el código, ejemplo family = Gamma(link = "log"). Si no se especifica una familia, gamm usa distribución gaussiana con función de enlace identidad. La ayuda ?gamm muestra todos los argumentos y los defaults.
Se observa que ambos términos de suavizado son significativos (p-value < 0.05), y el \(R_{adj}^{2}\) del modelo es 0.5640034.
Evaluación del modelo
windows()
par(mfrow=c(2,2))
gam.check(modelo1$gam, type="pearson")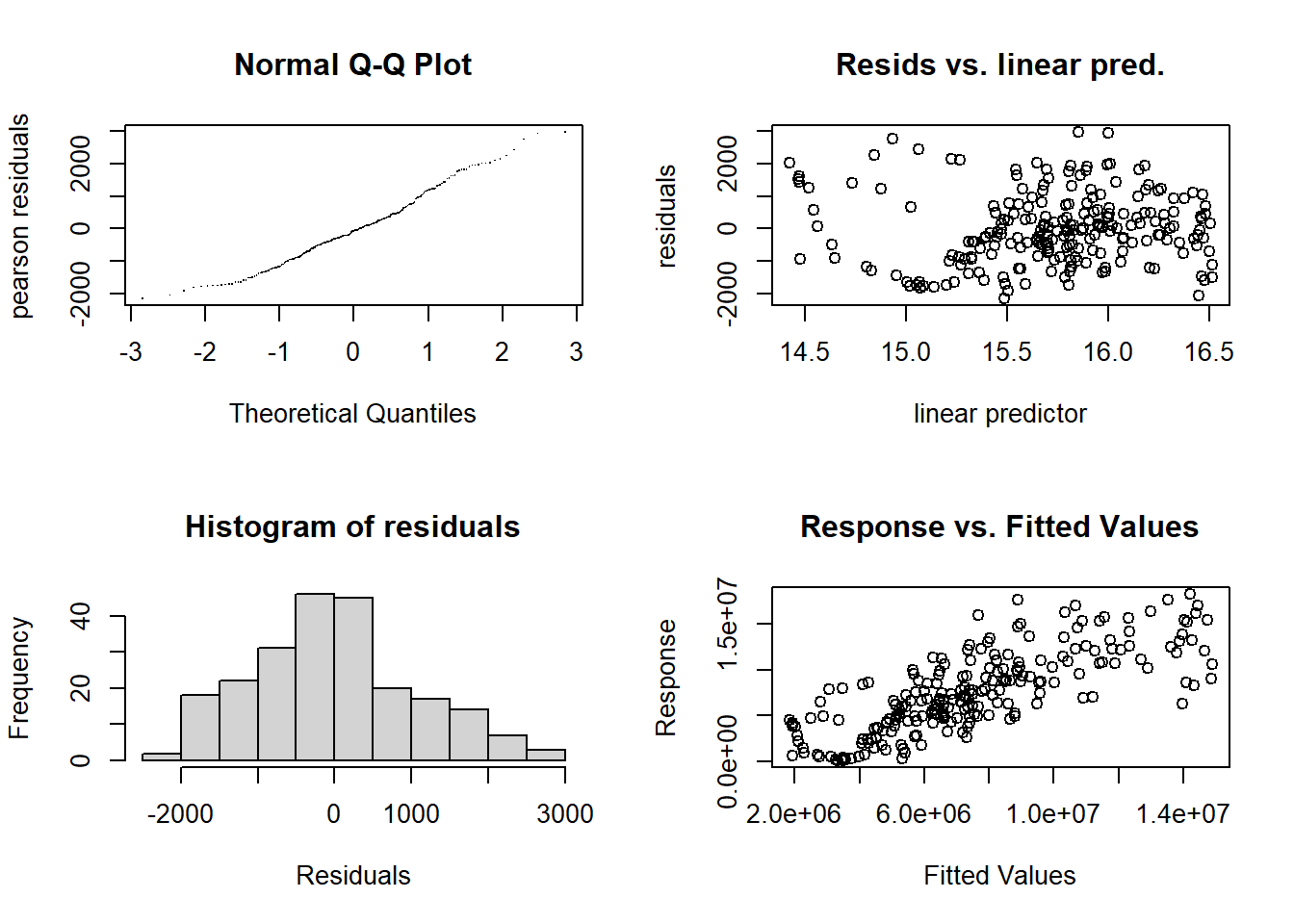
Figure 3.4: gam.check del modelo 1.
##
## 'gamm' based fit - care required with interpretation.
## Checks based on working residuals may be misleading.
## Basis dimension (k) checking results. Low p-value (k-index<1) may
## indicate that k is too low, especially if edf is close to k'.
##
## k' edf k-index p-value
## s(Mes) 8.00 3.86 0.93 0.13
## s(Dias) 9.00 8.74 0.31 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Los gráficos de la izquierda de la Figura 3.4 muestran que es correcto utilizar la quasi familia quasipoisson. El gráfico superior derecho muestra una dispersión bastante homogénea de los residuos, por lo que no habría mayores problemas con la varianza. El gráfico inferior derecho muestra una relación lineal positiva entre los valores observados y los predichos por el modelo. Si se logra mejorar el modelo, se observará una mejoría en este gráfico y en el \(R_{adj}^{2}\) del modelo.
En el modelo 1 no se especificó el k en los términos de suavizado s(), se utilizó la opción default k = 10. Este argumento especifica la dimensión de las funciones basis del spline. Cuando se indica un valor de k, este determina el máximo grado de libertad permitida para ese término del modelo. Sin embargo, los grados de libertad efectivos edf para cada término los estima el modelo a través de la penalización, siendo el límite superior \(k' = k - 1\). No especificar el argumento k equivale a indicar k = 10.
El gam.check() nos indica que el k del término s(Dias) del modelo 1 es muy bajo (valor de p-value bajo y edf cercano a k'. Ver ?choose.k para mas detalles.
Para mejorar el modelo se modifica k. Se disminuye k = 6 en s(Mes) para evitar que incrementen los edf de ese término, y se aumenta k = 20 en s(Dias). Además, se agrega un término de interacción ti() adecuando para trabajar con variables que tienen diferentes unidades (meses versus días).
modelo2<-gamm(Pcy_orgml ~ s(Mes, bs = "cc", k=6) + s(Dias, bs="cr", k=20)
+ ti(Mes,Dias, bs=c("cc","cr")), family=quasipoisson,
data = base, correlation = corCAR1(form = ~ Dias))##
## Maximum number of PQL iterations: 20## iteration 1## iteration 2## iteration 3Interpretación visual de los efectos parciales: curvas suaves s()( smooth functions)
plot(modelo2$gam, scale=0, scheme=1, pages=1)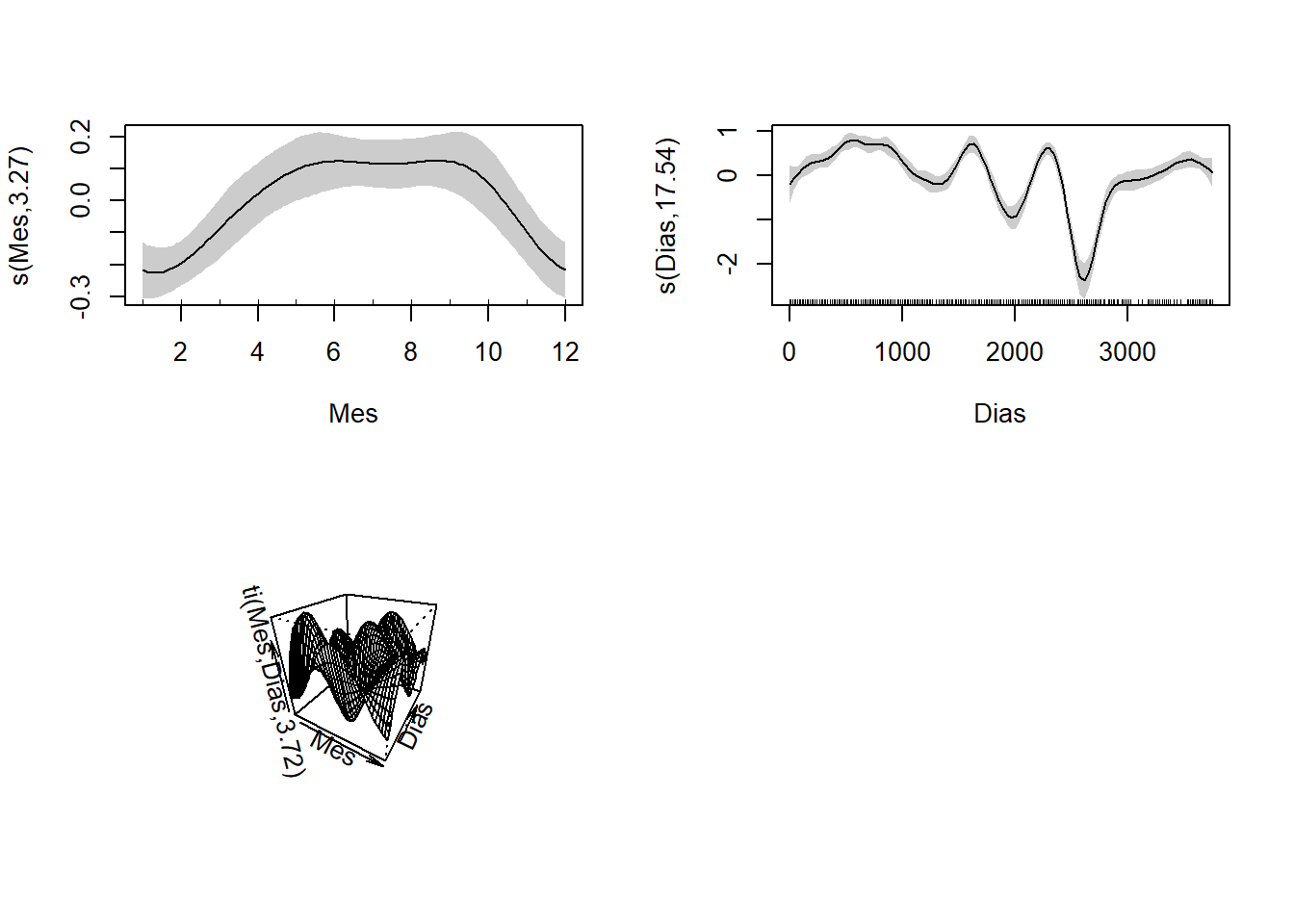
Figure 3.5: Efectos parciales del modelo 2. Las curvas suaves se centraron en cero, se indican los intervalos de confianza de 95% en gris. Las líneas internas en los ejes x (Mes y Dias) representan los datos.
La interacción se muestra en 3D, y es difícil de interpretar visualmente. Aquí nos centramos en la interpretación visual de los efectos parciales.
Información del nuevo modelo
summary(modelo2$gam)##
## Family: quasipoisson
## Link function: log
##
## Formula:
## Pcy_orgml ~ s(Mes, bs = "cc", k = 6) + s(Dias, bs = "cr", k = 20) +
## ti(Mes, Dias, bs = c("cc", "cr"))
##
## Parametric coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 15.64156 0.02398 652.3 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Approximate significance of smooth terms:
## edf Ref.df F p-value
## s(Mes) 3.268 4.00 9.085 <2e-16 ***
## s(Dias) 17.539 17.54 28.940 <2e-16 ***
## ti(Mes,Dias) 3.718 12.00 0.595 0.0395 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## R-sq.(adj) = 0.753
## Scale est. = 5.8774e+05 n = 225Los efectos parciales de s(Mes) y s(Dias) son significativos, y la interacción ti(Mes,Dias) es significativa. El \(R_{adj}^{2}\) del modelo aumentó a 0.7532274.
Evaluación del modelo
windows()
par(mfrow=c(2,2))
gam.check(modelo2$gam, type="pearson")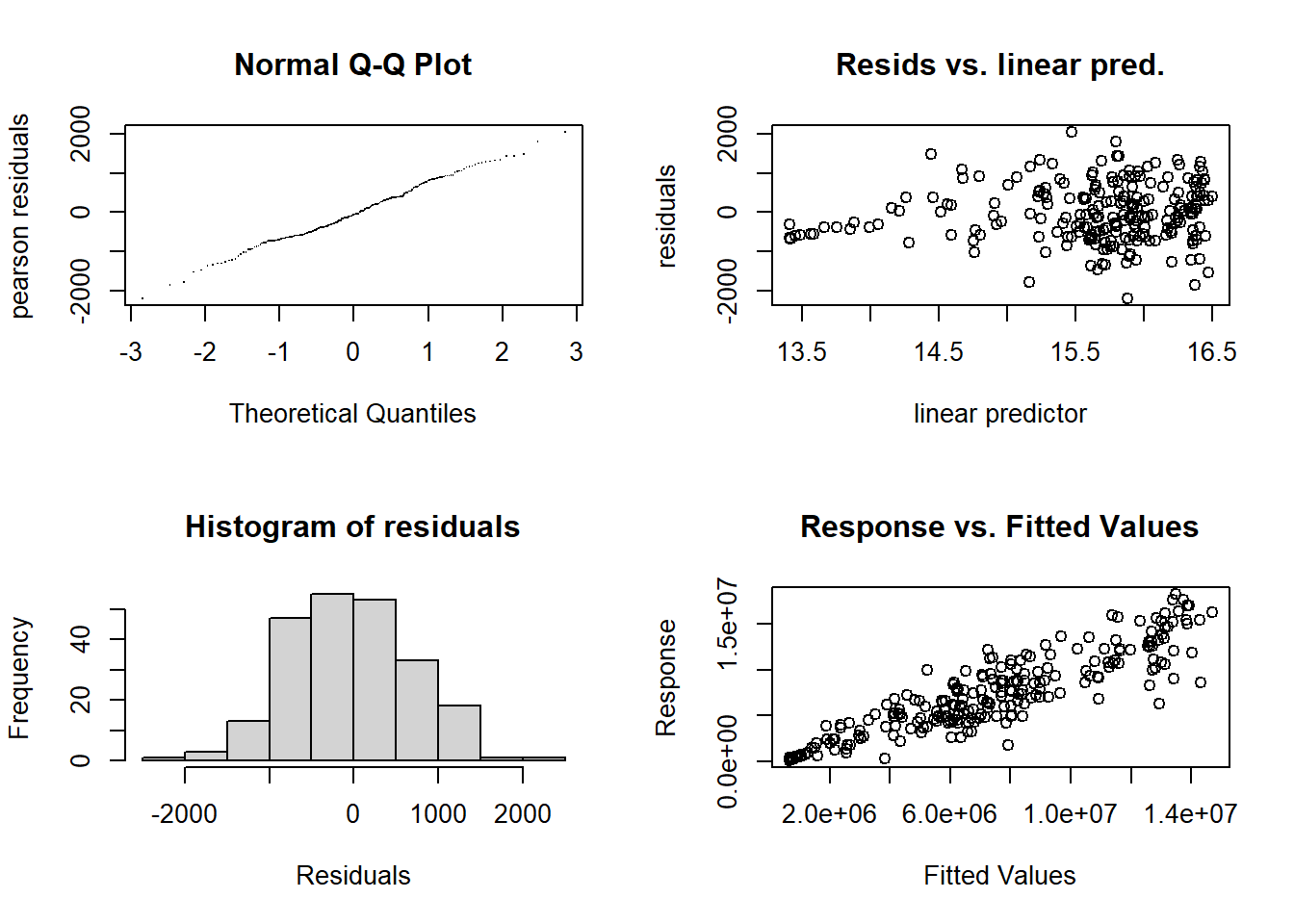
Figure 3.6: gam.check del modelo 2.
##
## 'gamm' based fit - care required with interpretation.
## Checks based on working residuals may be misleading.
## Basis dimension (k) checking results. Low p-value (k-index<1) may
## indicate that k is too low, especially if edf is close to k'.
##
## k' edf k-index p-value
## s(Mes) 4.00 3.27 0.84 0.005 **
## s(Dias) 19.00 17.54 0.66 <2e-16 ***
## ti(Mes,Dias) 12.00 3.72 0.89 0.015 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1De nuevo, parece correcto utilizar la quasi familia quasipoisson, sin mayores problemas con la varianza. La relación lineal positiva entre los valores observados y los predichos (gráfico inferior derecho) ha mejorado, coincidiendo con el incremento del \(R_{adj}^{2}\) del modelo.
Los edf del término s(Mes) son cercanos a 3, muy similares al primer modelo, lo cual corrobora que la especificación de k en el modelo no es crítica (modelo 1 k = 10, modelo 2 k = 6), siempre que se considere un límite superior adecuado. Para s(Dias) el p-value sigue siendo bajo y edf sigue cercano a k', pero k-index aumentó a 0.66. Se considera que no es necesario aumentar el k porque complejizaría el modelo, y consecuentemente la interpretación visual de la tendencia ( trend, efecto Dias).
Se pueden comparar ambos modelos estimando su AIC
AIC(modelo1$lme,modelo2$lme)## df AIC
## modelo1$lme 6 311.8362
## modelo2$lme 8 228.2012Efectivamente el modelo 2 presenta un AIC más bajo.
Otros gráficos
Se puede graficar con vis.gam().
vis.gam(modelo2$gam, type="response",
view=c("Mes","Dias"), main="Pcy (org/ml)",
plot.type = "contour", contour.col="black",color="terrain")
points(base$Mes,base$Dias,pch = 20) #agregar puntos de muestreo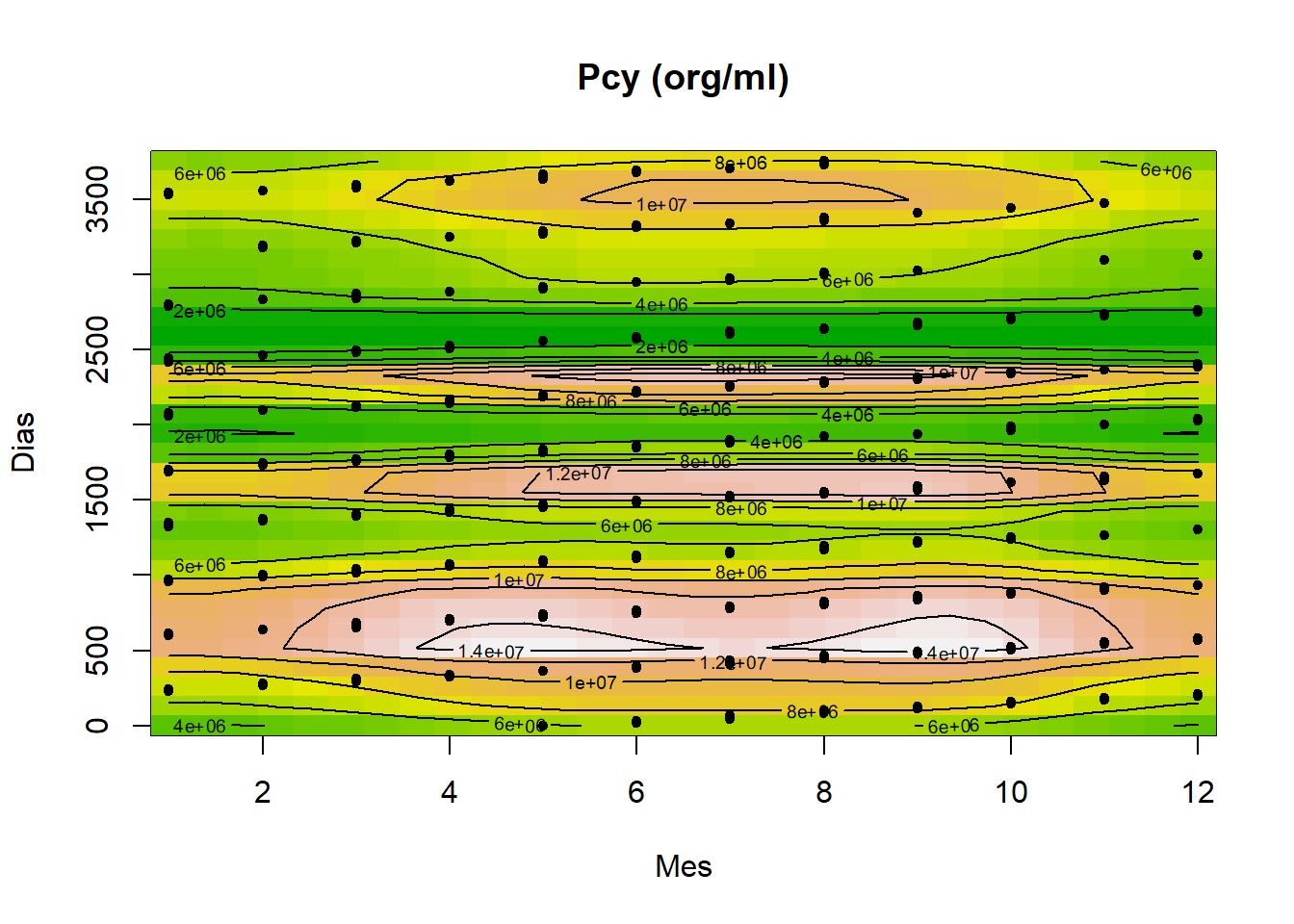
Figure 3.7: vis.gam plot del modelo 2.
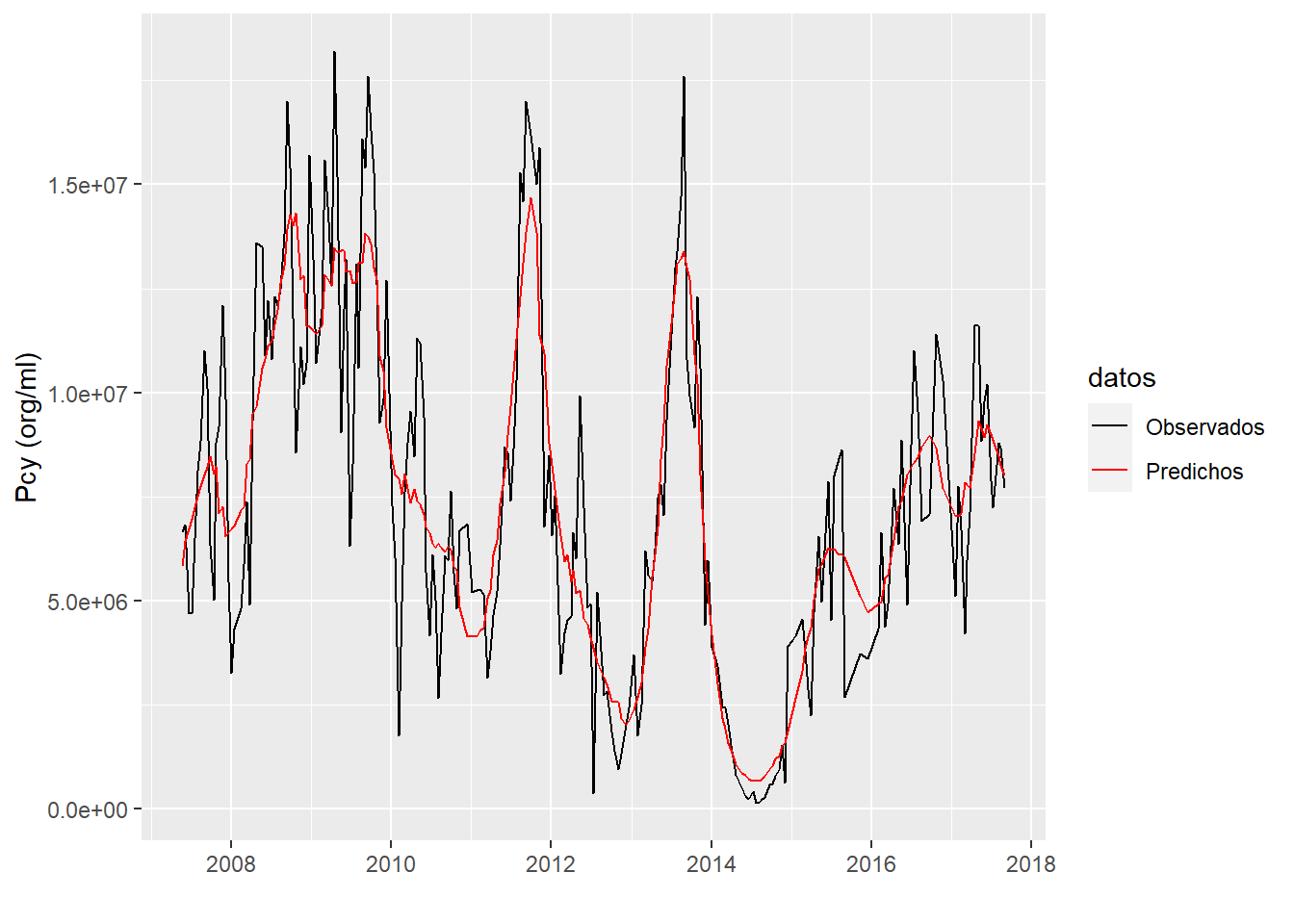
Se pueden graficar los valores observados a campo y los predichos por el modelo. Cuanto mas alto sea el \(R_{adj}^{2}\), mas similares serán ambos valores.
# generar datos para el gráfico
Base<-as.data.table(base)
datas <- rbindlist(list(Base[, .(Pcy_orgml, Fecha)],
data.table(Pcy_orgml = (modelo2$gam)$fitted.values,
Fecha = Base[, Fecha])))
datas[, datos := c(rep("Observados", nrow(Base)),
rep("Predichos", nrow(Base)))]
# generar el gráfico
ggplot(data = datas, aes(Fecha,Pcy_orgml, group = datos))+
geom_line(aes(colour = datos))+
scale_color_manual(values=c("black","red"))+
labs(x = "", y = "Pcy (org/ml)")